スクエア１中級解法パート６ 成形その２ - 汎用性の高い成形

　本記事はスクエア１中級解法シリーズのパート６に当たる記事です。

　本記事では成形手数の短縮に有用な汎用性の高い成形を紹介します。

偶数エッジ系の成形

　エッジが全て偶数個ずつ固まっているタイプの成形は、基本的にscallop - scallopに帰着すれば最短ルートからそう大きく外れることはありません。
　
　以下に偶数エッジ系成形の最短ルートの樹形図を示します。

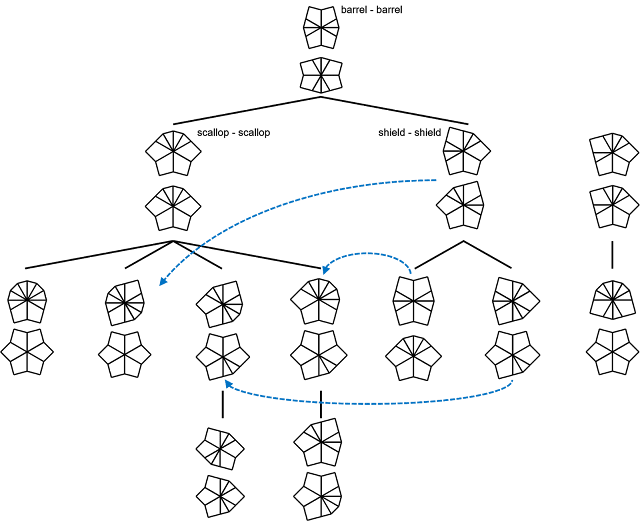偶数エッジ系の成形の樹形図（最短ルート）。shield-shield系統の成形は１手でscallop-scallop系統に移ることができます（青破線）。

図の通り、半分以上の成形はscallop-scallop→barrel-barrelのルートをたどるのが最短です。中にはshield-shieldに帰着するほうが短いものもあります。
　初めのうちは偶数エッジ系の成形はとりあえずscallop-scallopにまとめるようにしておいて、慣れてきたらshield-shieldの系統を覚えてみると良いでしょう。
　ちなみに 6-2 - star は例外的にこの樹形図から浮いていますが、これはstar成形なのでもう覚えていることでしょう。今まで通り処理してください。

5-1 - paired edges・5-1 perpendicular edges

　私が個人的にお勧めする超便利成形がこの2つです。これらはどちらも１手でkite-scallopに帰着できます。

5-1 - paired edgesと5-1 - perpendicular edgesの成形

　この２つの成形が便利なのは、難しい成形の多くのパターンが1, 2手でこのどちらかに帰着できるからです。功さんのブログの樹形図を見ると、特に5-1 - paired edgesの下に多くの成形がぶら下がっていることがわかります。最短ルートでさえこれですから、ひとまず最短を目指すことを置いておけば相当数の成形をカバーできるでしょう。

　偶数エッジ系以外の成形はひとまず5-1 - paired edgesか5-1 - perpendicular edgesのどちらかに帰着することを考えてみましょう。

　ところで5-1は3 corners（片面にコーナーパーツが3つ）の形なので、その対面はpaired edges・perpendicular edges・parallel edgesの3パターンしかありません。5-1 - parallel edgesの処理もついでに覚えてしまいましょう。非常に簡単で、1手で5-1 - perpendicular edgesに帰着するのが最速です。

5-1 - parallel edgesの成形

　これで、偶数エッジ系以外の成形はとりあえず片面に5-1を作っておけば大丈夫という状態になります。

　今回紹介する成形は以上です。
　これらの成形を覚えたら、あとは練習の過程で各成形の最短ルートの手順を少しずつ覚えていってみてください。覚える順番は手数の少ないものから網羅していくのでもよいですし、うえしゅうさんの記事のように類似の形をシリーズにして覚えていくのでもよいでしょう。拙作スクエア成形botもどうぞよろしく。

　多くの方は最短でも5手以上かかるような長手数の成形を覚えるのに苦労すると思います。次回の成形の記事では、そのような長手数成形を処理するための考え方をいくつか紹介します。