本記事では長手数を要する難しい成形の手順を覚えやすくする、あるいは記憶がおぼつかない成形手順をインスペクション中に思い出すための考え方をいくつか紹介します。
/1,0/系の操作によるエッジ位置の切り替え
/1,0/ やその上下・左右対称の操作(/-1,0/、/0,1/、/0,-1/)は、その回しやすさのため長手数成形の最適手順中にしばしば現れます。この操作がスクエア1の形状に与える影響を把握しておくと、多くの長手数成形を体系的に処理できるようになると思います。
実例を用いて説明していきます。例としてpawn - kiteの成形を考えてみましょう。(スクランブル:/-3,0/-2,-1/2,0/3,0/2,-3)
このスクランブルの成形手順(の一例)は -2,-3/1,0/-4,0/-1,0/-3,0 です。 赤太字で書いた/1,0/の前後でのスクエア1の形状の遷移に注目してみましょう。実際に成形手順を回して観察してみて下さい。
すると、下図のように/1,0/の前後ではU面のスラッシュ位置の隣にあったエッジが1つD面に移動し、一方D面のスラッシュ位置の隣にあったエッジが1つU面に移動していることがわかると思います。
ここで、パーツの移動という見方は一旦忘れて、純粋に形状の変化だけをU,D面それぞれで観察してみます(上図の下半分・上半分をそれぞれ隠してみると良いかも)。
すると、U面ではスラッシュ位置の隣にあったエッジが1つ取り除かれ、代わりにその対角位置にエッジが1つ付け付け加えられていることがわかります。一方D面でも同様に、スラッシュ位置の隣にあったエッジが1つ取り除かれ、代わりにその対角位置にエッジが1つ付け加えられています(伝われ)。
結局、/1,0/やその上下・左右対称の操作は、UD面のそれぞれで、スラッシュ位置の隣にあるエッジを1つ取り除き、その対角位置にエッジを1つ付け加える作用があるものとみなすことができます(下図)。pawn - kite の場合はこれにより、簡単な3手成形である shield - square に帰着されています。
逆に言えば、「UD面のそれぞれでエッジを1つ取り除き、その対角位置にエッジを1つ付け加える」ことによって簡単な成形に帰着できる形は、/1,0/系の操作が有効だということになります。この作用を適用したいエッジをAUDFでスラッシュ位置の隣にセットアップし、/1,0/、/-1,0/、/0,1/、/0,-1/ の中から適当なもの選んで回せばよいわけです。
次の例として mushroom - pawn の成形を考えてみましょう。(スクランブル:/-3,-3/0,-1/-4,0/4-5/)
この成形を「UD面のそれぞれで、エッジを1つ取り除きその対角位置にエッジを1つ付け加える」ことによって簡単な成形に帰着することはできないでしょうか。
しばらく考えると、この成形は scallop - scallop に帰着できそうであることに気づきます。では、どのようなAUDFをして、/1,0/、/-1,0/、/0,1/、/0,-1/ のうちどれを使えば scallop - scallop に帰着できるでしょうか。
正解は 5,0/0,1/ です(もしくは -1,6/1,0/ でもOK)。
scallop - scallop に帰着できたら、あとは普通に成形するだけです。結局このスクランブルの成形手順は 5,0/0,1/0,-2/-2,-1/3,3/ (もしくは -1,6/1,0/0,-2/-1,-2/-3,-3 など)となります。
このように /1,0/ やその上下・左右対称の操作によって簡単な成形に帰着できるパターンは 4 corners(UD面それぞれにコーナーが4つある成形) のものに多くあります。以下の表にその例をまとめておきます。
実用上は、どのパターンがどの簡単な成形に帰着できるのかを前もって覚えておき、AUDFと適用する/1,0/系の操作はインスペクション中に場当たり的に考えれば十分通用すると思います。実例を用いて説明していきます。例としてpawn - kiteの成形を考えてみましょう。(スクランブル:/-3,0/-2,-1/2,0/3,0/2,-3)
 |
| pawn - kite |
すると、下図のように/1,0/の前後ではU面のスラッシュ位置の隣にあったエッジが1つD面に移動し、一方D面のスラッシュ位置の隣にあったエッジが1つU面に移動していることがわかると思います。
 |
| /1,0/部分でのpawn - kiteからの遷移 |
すると、U面ではスラッシュ位置の隣にあったエッジが1つ取り除かれ、代わりにその対角位置にエッジが1つ付け付け加えられていることがわかります。一方D面でも同様に、スラッシュ位置の隣にあったエッジが1つ取り除かれ、代わりにその対角位置にエッジが1つ付け加えられています(伝われ)。
結局、/1,0/やその上下・左右対称の操作は、UD面のそれぞれで、スラッシュ位置の隣にあるエッジを1つ取り除き、その対角位置にエッジを1つ付け加える作用があるものとみなすことができます(下図)。pawn - kite の場合はこれにより、簡単な3手成形である shield - square に帰着されています。
 |
| 「UD面のそれぞれで、スラッシュ位置の隣にあるエッジを1つ取り除き、その対角位置にエッジを1つ付け加える」のイメージ。 |
逆に言えば、「UD面のそれぞれでエッジを1つ取り除き、その対角位置にエッジを1つ付け加える」ことによって簡単な成形に帰着できる形は、/1,0/系の操作が有効だということになります。この作用を適用したいエッジをAUDFでスラッシュ位置の隣にセットアップし、/1,0/、/-1,0/、/0,1/、/0,-1/ の中から適当なもの選んで回せばよいわけです。
次の例として mushroom - pawn の成形を考えてみましょう。(スクランブル:/-3,-3/0,-1/-4,0/4-5/)
 |
| mushroom - pawn |
しばらく考えると、この成形は scallop - scallop に帰着できそうであることに気づきます。では、どのようなAUDFをして、/1,0/、/-1,0/、/0,1/、/0,-1/ のうちどれを使えば scallop - scallop に帰着できるでしょうか。
正解は 5,0/0,1/ です(もしくは -1,6/1,0/ でもOK)。
 |
| 5,0/0,1/とした場合の mushroom - pawn → scallop - scallop の遷移 |
このように /1,0/ やその上下・左右対称の操作によって簡単な成形に帰着できるパターンは 4 corners(UD面それぞれにコーナーが4つある成形) のものに多くあります。以下の表にその例をまとめておきます。
ですが、その操作の探し方は私は感覚的にやっていていまひとつ言語化しにくいところです。これに関しては各自で体得してもらう他ありません。
該当するものを(前後・左右対称のものは除いて)網羅しましたが、中には1手でstarに帰着しているものや、1手で5-1 - paired edges に帰着していると見なせるものもあります。自分が覚えやすいように覚えてみてください。
/1,0/系の操作と比べると該当パターンが少なく(というか恐らくこの1パターンだけ?)汎用性は低いですが、それでも成形の最適手順を覚える上での一助にはなるでしょう。
このスクランブルの成形手順は 2,-3/-2,0/2,0/-1,0/-3,0/ です。赤太字で書いた/-2,0/の部分での変形に注目しましょう。
すると、U面のshieldのコーナーが3つ連続した部分を利用することで、U面側の形に影響を与えずにkiteの右半分のL-shapeが逆向きに変更されていることがわかります。これによりshield - kiteは3手成形であるshield - squareに帰着されています。
このように一方の面に3 cornersがあるパターンでは、もう一方の面にあるL-shapeだけを逆向きに変更することができます。
同様の考え方は scallop - square にも適用できます。
余談ですが、pawn - fist の easy or bad の判断は私の場合「片面にkiteを作れる位置にAUDFしたときに、エッジのペアが2つともスラッシュ面の隣に来るかどうか」で行っています。隣に来ればeasy、来なければbadです(文面だけで伝えるのは苦しい)。
このスクランブルの成形手順の例は 4,0/0,2/-4,0/-1,4/-3,0/ です。赤太字で書いた/0,2/の部分でエッジペアの位置をずらし、3手成形のeasy pawn - pawnに帰着しています(下図)。
同様の考え方はshield - scallop → scallop - scallopの帰着やmushroom - scallop → kite - scallopの帰着などにも適用できます。これらはそれぞれ偶数系エッジのパターンと1手で5-1 - paired edgesに帰着するパターンであり今更目新しさはないかもしれませんが、それでも2スラッシュ分を一連の動きとしてとらえることができるため手順の見通しは良くなるように思います。
| 成形 | 操作 | 帰着先 (AUDFは合わせていません) |
| /0,1/ | ||
| /1,0/ | ||
| mushroom - pawn | /-1,0/ | scallop - scallop |
| /1,0/ | ||
| /0,1/ | easy pawn - pawn | |
| /-1,0/ | scallop - scallop | |
| /-1,0/ |
該当するものを(前後・左右対称のものは除いて)網羅しましたが、中には1手でstarに帰着しているものや、1手で5-1 - paired edges に帰着していると見なせるものもあります。自分が覚えやすいように覚えてみてください。
/2,0/系の操作によるエッジ位置の切り替え
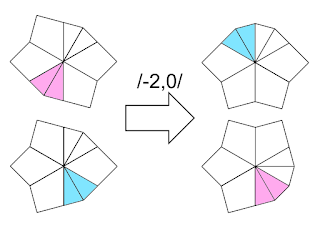
前節の応用として、エッジ2つのペアに対しても同様の考え方を適用することができます。例えば barrel - shield は下図の向きから /-2,0/ とすることで scallop - scallop に帰着できます。/1,0/系の操作と比べると該当パターンが少なく(というか恐らくこの1パターンだけ?)汎用性は低いですが、それでも成形の最適手順を覚える上での一助にはなるでしょう。
3 cornersを利用したL-shapeの向き変更
shield - kiteの成形を考えてみましょう。(スクランブル:1,-1/0,-3/-3,-2/0,-2/6,-4/4,3)このスクランブルの成形手順は 2,-3/-2,0/2,0/-1,0/-3,0/ です。赤太字で書いた/-2,0/の部分での変形に注目しましょう。
すると、U面のshieldのコーナーが3つ連続した部分を利用することで、U面側の形に影響を与えずにkiteの右半分のL-shapeが逆向きに変更されていることがわかります。これによりshield - kiteは3手成形であるshield - squareに帰着されています。
このように一方の面に3 cornersがあるパターンでは、もう一方の面にあるL-shapeだけを逆向きに変更することができます。
同様の考え方は scallop - square にも適用できます。
3 cornersを利用したエッジペアの位置ずらし
前節で紹介した3 cornersの利用の仕方に似たものとして、エッジペアの位置ずらしがあります。例として bad pawn - fist の成形を考えてみましょう(スクランブル:1,-1/-3,0/5,-2/0,-4/-2,-4/-4,0)。余談ですが、pawn - fist の easy or bad の判断は私の場合「片面にkiteを作れる位置にAUDFしたときに、エッジのペアが2つともスラッシュ面の隣に来るかどうか」で行っています。隣に来ればeasy、来なければbadです(文面だけで伝えるのは苦しい)。
このスクランブルの成形手順の例は 4,0/0,2/-4,0/-1,4/-3,0/ です。赤太字で書いた/0,2/の部分でエッジペアの位置をずらし、3手成形のeasy pawn - pawnに帰着しています(下図)。
同様の考え方はshield - scallop → scallop - scallopの帰着やmushroom - scallop → kite - scallopの帰着などにも適用できます。これらはそれぞれ偶数系エッジのパターンと1手で5-1 - paired edgesに帰着するパターンであり今更目新しさはないかもしれませんが、それでも2スラッシュ分を一連の動きとしてとらえることができるため手順の見通しは良くなるように思います。
7手成形とその経路上の成形の暗記
スクエア1の成形に要する最長の手数は7手であり、該当パターンは kite - squareの1通りしかありません(スクランブル:/3,0/1,0/-2,0/2,0/-2,0/1,0/)。
これは割り切って暗記してしまいましょう。成形手順は下図の左端の向きから /-1,0/2,0/-2,0/2,0/-1,0/-3,0/ です。
 |
| kite - square の成形手順中での遷移図 |
実際に回してみると(回さなくても手順の回転記号を見れば)わかりますが、一切D面を回すことなく成形できる非常に回しやすい手順です。
遷移をよく観察してみると、まずkite - squareから/-1,0/の操作によりshield - kiteに帰着、さらにshield - kiteから3 cornersを利用したL-shapeの向きの変更によりshield - squareに帰着、という手順の構造になっていることがわかります。今回の記事で紹介した考え方の組み合わせになっていることに注意すれば、手順を覚えるのにさほど苦労することはないでしょう。
また、上記の遷移図の途中に現れている成形もあわせて覚えてみてください。これらも当然D面を一切回さずに成形できるパターンです。
今回の記事で紹介する成形の考え方は以上です。成形手順の暗記を苦行だと感じている方は少なくないと思いますが、これらの考え方を参考にしてがんばってみてください。
本シリーズで個別に触れていない成形のパターンはまだたくさんありますが、そのほとんどが本シリーズで扱った成形のパターンに1手で帰着できるはずです。残りの成形は各自で地道に覚えていってみてください。成形の8割以上を最短手数でこなせるようになれば、タイムがかなり安定してくるはずです。
遷移をよく観察してみると、まずkite - squareから/-1,0/の操作によりshield - kiteに帰着、さらにshield - kiteから3 cornersを利用したL-shapeの向きの変更によりshield - squareに帰着、という手順の構造になっていることがわかります。今回の記事で紹介した考え方の組み合わせになっていることに注意すれば、手順を覚えるのにさほど苦労することはないでしょう。
また、上記の遷移図の途中に現れている成形もあわせて覚えてみてください。これらも当然D面を一切回さずに成形できるパターンです。
今回の記事で紹介する成形の考え方は以上です。成形手順の暗記を苦行だと感じている方は少なくないと思いますが、これらの考え方を参考にしてがんばってみてください。
本シリーズで個別に触れていない成形のパターンはまだたくさんありますが、そのほとんどが本シリーズで扱った成形のパターンに1手で帰着できるはずです。残りの成形は各自で地道に覚えていってみてください。成形の8割以上を最短手数でこなせるようになれば、タイムがかなり安定してくるはずです。


















0 件のコメント:
コメントを投稿